SRAM, let's try that again

Are we allowed to cheat a little?

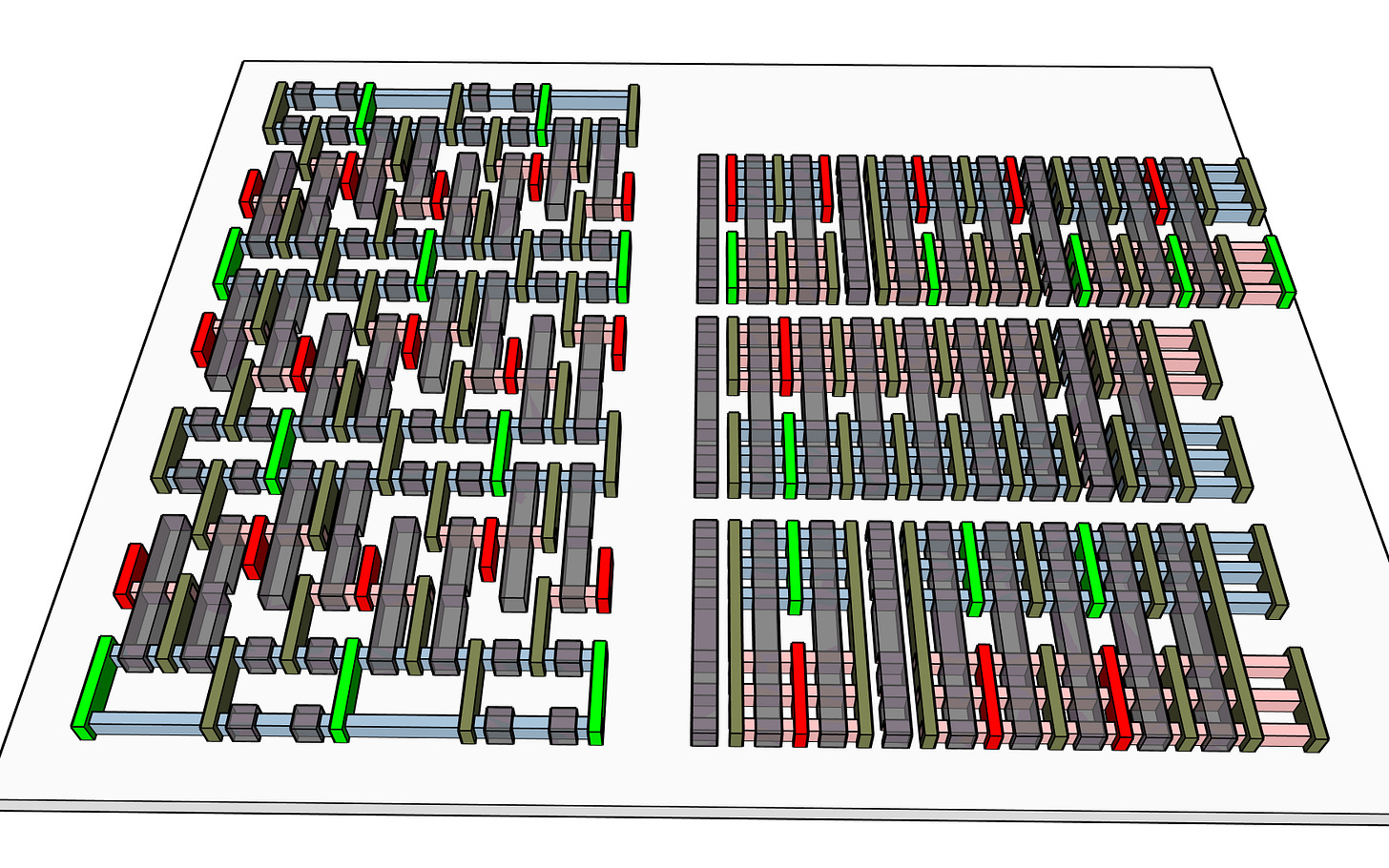
In last week’s post the strict use of Mock 4 rules did not produce a satisfactory result. The wires are too thin and crowded. It is not a good start. If we look at the literature on SRAM they publish some shadowy images of the devices where it is hard to make out details but it does appear fairly consistent that they do a better job of the crosstalk wiring than my first draft did. What would it take for us to be able to route the crosstalk more directly? Since the drain and the gates are adjacent it is very tempting to find a way to cheat but remain in principle compatible with Mock 4 logic.

Let’s look at logic beside the SRAM region and how the fins and low-level structures are made. The fins line up with the SRAM region using only every second fin. The SRAM fins need space between to allow split gates and split contacts on the fins and that can't be done if they are at the finest pitch.

In logic the fine pitch fins are all N-fins or P-fins bound together to act as one transistor. There is a missing fin between the P-fins and the N-ins, to provide space for split elements if necessary. In the SRAM there are split function in every cell and weak 1-fin transistors so it has just half the fin density of the logic.

If we outline and label the logic and the Sram you can see a D FlipFlop is far larger than an SRAM cell, even though both hold just 1 bit.

Now let's look at another difference between the SRAM and the logic. This is where I begin cheating. But it isn't really cheating if the lithography works.

Stubs are inserted in the fins where logically the fins are cut. The fins on the logic are now completely continuous. The sections in lighter color are biased non-conductive by tying their gate to the nearest power line. This is to maintain uniform stress along the fins. Stress is an essential part of the construction of modern FinFET (see the excellent comment by Greg Taylor on the previous post). The amount of stress is extremely high so if the fin is really cut the stress relaxes and the electrical properties are degraded. So on the logic side there are no real cuts in the fins.

However on the SRAM you can see I've proposed that there are real cuts made between in certain parts of the P fins.

The proposal is to cut the FIN but leave a stub on the end so there will be some stress still working. Can this really be done? The lithography pattern is sparse on both the SRAM and the logic, which should allow for a good amount of inverse lithography transform (ILT) in the mask to allow a compromise illumination valid for both.

This is going to reduce the drive on the P-FETs in the SRAM cells, but that is not a bad thing as long as the resulting performance is in the range of half as good. SRAMs ideally do have weaker P-FETs in the inverter pair.

Let’s look at how this enables a better feedback solution. The cuts allow the bias gates to be removed so that the inverter gates can be lengthened. The inverters will not short out to the neighboring cell because of the true cut. We will not really care how the stub and the extended gate interact because the next step wires the gates to the drain contacts anyway.

That is it. No further rules need to be “broken” as we construct the rest of the cell. The cross connect signal is using the gate polysilicon as an extra connection layer bypassing M0 from below for this special case, leaving M1 open for other uses.

The M1 connections tie the word-enable gates together and also help build vertical routes to the M2 layer which is used for longer runs of enable, power, and ground.

Notice that the peculiar Mock 4 rules of 45nm pitch for M2 do not line up exactly with the 240nm height of the SRAM row of cells, but the M2 layer is empty enough that we can slightly modify it to suit each row. If the runs are long then some or all of the M2 lines could be mirrored or alternated to M4 to reduce capacitive coupling. We could also use M2 to make occasional ties between M1 power lines, and M1 ground lines, which would improve both reliability and avoid droop (since most rows are passive in any cycle, they provide capacitance which is a good thing on power lines).

The data lines, DQ and ~DQ, will run top to bottom on M3.

These can be nicely spaced to reduce capacitance. In a real world design we might alternate or double them to the M5 lines.

And that is it, done.

If you flip back to the previous post you will see how much cleaner this design is. It also looks like a good baseline for adding functionality.

Here it is again in a video!

Summary

A single port can either write or read using both DQ and ~DQ to set or read the data. It cannot do both operations at the same time, but it is the most compact form of SRAM. That functionality might work fine for dual buffers, where two arrays are in use - one being read while the next data is being written into the other, swapping roles when they reach their ends, and for a few other things. It is not popular for caches where there are generally at least 2 ports so that an external facing interface to the system fabric can run mostly independent (they need rules for handling simultaneous use of the same row) random access without needing buffers to wait for the other side. It certainly is not useful for registers which tend to start with a minimum of 2 independent readers and one writer for a simple core, and can add even more ports in a high performance core. So, let’s look next at how extra ports work and how they change the size of a cell.

References

Prof. Franz Kreupl pointed me to this nice paper Intl 2014 FinFET SRAM in which you can clearly see the fin and gate structure (but the source and drain contacts are absent, as are all metals) confirming the feasibility of cutting the P fin in just the place I predict.

This thesis by Dr. Yokoyama (2020)is a lucid recent discussion of SRAM design and includes discussion of write assist.

A recent 5nm TSMC 5n SRAM (2021) design is presumably close to recent practice.

Next Week

Next week we look at adding functionality (ports) to the design. We will also start looking at the edge circuits needed to make the array useful.

In the week after, the floorplan for a small array including its edge circuits will be sketched with some calculations for overall cell size per bit at different sized arrays.

New Poratbo posts will be released on Mondays. All posts in this series are unlocked, but paying subscribers see them a week earlier.