Slides Rule

Slipstick intelligence?

Oct 28, 2024

A recent article about approximating multiplication with addition caught my attention. It reminded me of engineering calculations before electronics.

circular slide rule

The idea used a trick well known for calculating transcendentals like logarithm, which is that the first few bits of the mantissa (fraction) part of a floating point number are usefully close to Log2(1 + fraction). Or to put it differently, the curve of Log2 function for the range 1.000 .. 1.999 is not very curved. This true for a number of other functions, so when making approximations several function approximations just start with the fraction, then calculate some corrections.
And that indeed is what Dr. Bamania did, he worked out a very simple set of corrections that get close to matching a multiply. But not exactly, and that bugged me, so I started playing with the numbers.

Just Use the Real Thing

Then I realized this approach could be reversed. Instead of sort-of kind-of using logarithms why not really use them? Instead of FP8 with E5M2 or E4M3 formats, what if we used Exp8, an 8 bit logarithm rounded to either E5.2 of E4.3 formats, two or three bits of fraction? Use these as the primary data type. The FP8 numbers used in AI are mostly approximations anyway, and the Exp8 approach would have the advantage of a constant proportional error, in return for having fewer exact matches to integers.

Call it log or call it exp? Although log is perhaps more accurate, the existing FP literature uses “exponent” and “mantissa” so using “exp” makes it easier to see how formats are related.

The big advantage is that adding the Exp8 representations of x and y now gives an exact multiply, x * y, by addition. It is also easy to mix E5.2 and E4.3, then Exp6 and Exp4 all follow the same design, mixing is just a matter of aligning the binary-point. The result needs to have at least 6 bits for the exponent, but we will get to the design of the running totals in a moment.

.. and then Fix It

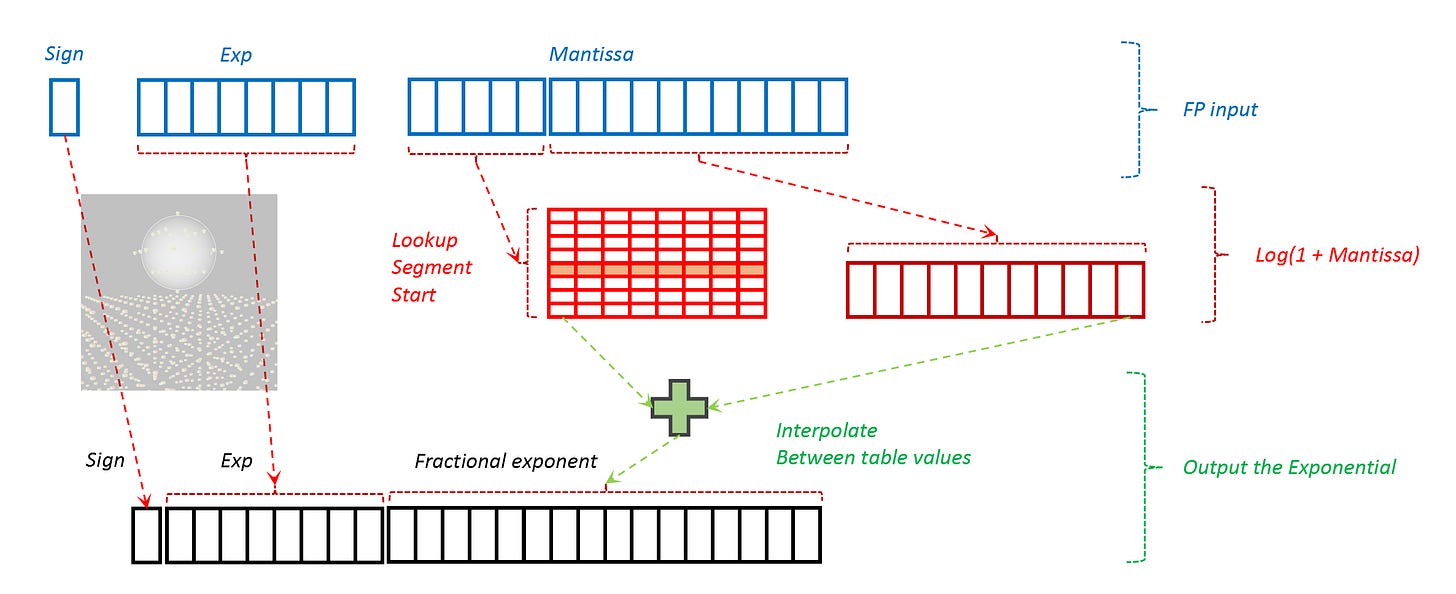
The dominant operation in AI is the fused multiply-add (FMA). The multiply is simple and efficient now, but to do the addition the value needs a linear mantissa. This can be implemented with a simple look-up. There are at most 3 bits of log fraction for Exp8 so an 8-entry ROM can convert a product into a classic FP form. We will draw the lookup circuit a little later in this blog post, but for now just take my word for it, a lookup table is smaller than an adder, quite compact and low power. Also, the values can easily be made wide to give good accuracy to the multiply. 6 bits would be about the same accuracy as the conventional FP8 multiply.

If FP8 is used both inputs need tweaks before adding and still the result was not completely accurate. When using Exp8 values the multiply is exact, various input formats all combine directly without tweaks, and the output needs just one easy low-power lookup to get an accurate mantissa.

.. and then Covert It Back

The vast majority of the multiply-add operations in an AI model occur in tensor reductions where we eliminate a pair of row/columns by multiplying the elements pair-wise and adding up the total for all of the column or row. This can be a lot of pairs and so the summation is usually a larger arithmetic type, an FP16 or even FP32, to capture the result without overflow or too much lost precision from underflow. The summation mechanism likely has at least 16 bits of fraction and 8 bits of exponent. It will generally stay in that larger format to be processed by non-linear functions that limit extremes or calculate probability functions.

Conversion back into Exp8 might rarely be needed. But, if it does, if it is found useful to recirculate with Exp8 format, conversion is not expensive and normally such conversions will be needed for a tiny fraction compared to the FMA rate.

The log function can be approximated by linear functions. The first few bits of an FP16 or FP32 mantissa can be used to drive a lookup table and then the rest of the fraction is used for interpolation, with one or two shift-and-add operations to provide the correct slope for the interpolation. This logic is compact enough to be provided in every pipeline and remain a minor burden on the computation pipeline.

The interpolation may add or substract more than one shifted version of the mantissa remainder, to match for the slope of that CORDIC approximation.

Division is Easy Too

I’m not sure how useful it will be, but division is like multiplication with one operand negated before going into exactly the same FMA machinery. If you have ever wanted to do that, a lot of that in tensor form, it could be possible.

Zeros and Infinity

Zero exponent should be treated as a zero, circumventing the adder.

This leads to a question of how to use the sign bit for a zero. My intuition is:

A zero exponent with a zero sign bit is a true zero.
A zero exponent with a 1 for sign bit is an infinity.
You would create an infinity only by dividing by zero, or as the result of an unbounded overflow in converting from a larger number.
Infinity is affine, not signed. Dividing by infinity gets you back to zero.

A signed zero is always useless, while infinity is useful sometimes.

Share Poratbo

Should Exp16 be a thing?

There is a possibility to do the same thing for multiplying a 16-bit format. The first 4 or 5 bits of the summed exponent-fraction would drive a lookup table which includes shift and add alignment for interpolation to get an accurate linear value. It would still enable an energy-efficient FMA. I leave it as an exercise for the interested reader.

The Width of the Sum

Let’s return to considering why the sum of the tensor arithmetic is a bigger data type. Tensors in modern AI can have dimensions in the thousands, so when values are added the sums can be hundreds or thousands of times larger than the average value. If the summation data type is too small, then new values are rounded down to zero instead of contributing to the sum. A wide summation type minimizes that error.
A consequence of this is that the Add will use more energy and silicon than the multiply! We could use an 8 bit add to multiply Exp8 format, but then need an FP32 type for the summation. This is unavoidable even if the values are 6-bit or 4-bit, we still need an accumulation type that is 10 to 16 bits wider than the elements. Exp8 will get very close to the minimal energy for FMA operations, with accuracy and flexibility to mix data widths.

Building a Lookup Table

I will close with some circuits for a lookup table. It is likely there are even more compact solutions known, since lookups are a very old function type that get used a lot. This design here is simply an estimate.

The E4.3 format will require an 8-way lookup table. This will have 8 rows. Each row has a pattern match prefix, and a value delivery suffix. The prefix is a pattern match on one of the values from 000b .. 111b. When the pattern does not match, the output of the prefix turns off all the transistors in that row’s suffix. When the pattern does match, which it does for exactly one row, the suffix transistors are turned on.

The values are wires connected vertically across all 8 rows, with one transistor per row. It is either a PFET connecting the wire to the positive rail, or an NFET connected to the negative rail. Each row of the table in this design, which delivers a 5 bit value, is 19 x CPP wide and 1 rail high. Adding a 6th value bit would make it 20 wide. For 8 rows that is about 1 square micron in a 2nm process with GAA/ribbon FETs. On average 30 transistors transition for each lookup operation, which should be less than 2 femto-Joule of switching energy. About 4M of these would be needed on a GPU which processes 16 PFLOPs of FMA at 2GHz, which total about 4 mm2 of area and consume 16W of power - very much back-of-the-envelope estimates for now.

The 6-bit values for a 3-bit fractional exponent have a worst-case error of 0.3% and an average error of 0.11%. 7-bit values have the same worst-case but an average error of 0.004%. 8-bit values have a worst-case error of 0.14% and an average error of 0.01%. One could make a reasonable engineering trade-off argument for any of these widths, since the energy difference for 8 bits is a small fraction of the overall FMA energy, but on the other hand polishing a 3 bit fraction to 9 bit precision seems like overkill. The 7-bit lookup table looks interesting with its miraculously small average error.

The 8-bit exponent adders and the fraction accumulators will each be multiples larger and consume more energy than the lookup tables.

Making it Real

Well, as real as a finite precision can be…

It will not be easy to test Exp8 since no existing chip is set up for logarithmic arithmetic and approximations. It should be possible to use FPGAs to build fast enough tensor processors to run comparisons on the accuracy and equivalence of tensor operations compared to FP8 or even BF/FP16. Actually we could do that with CPUs or GPUs, much slower than FPGAs but time to first results may be shorter since the development tools are more productive, and saving a few days time on development is more important than saving some hours of CPU time for simulations.

If the basic tensor operations prove comparable then it may be worth proceeding to the next step of Verilog/RTL design for something like a 32 x 32 MatMul unit to validate estimates for area and power.

If these look good, maybe time to tape out a chiplet, maybe something of a scale which might be useful for inference. There would be a lot more work needed to make use of Exp8 in training, since 8-bit training is fairly new and can be less stable than 16 bit, and the training chips tend to be more complex so teams will see a new format as a disruption to other goals and timelines.

However, I do think Exp8 has the potential to be the least power way to implement a stable 8-bit data type for AI models, with provision for 6-bit, 4-bit, and microscaled weights easily mixed in too.

Poratbo