In the last post the scope of the cell library was described. It will be for static logic design, with around 30 of the most useful and optimizable logic building blocks, including some of the circuits for clocking and latches, and the largets cells will be full adders. Now we get started.
This is the first post on Poratbo which is partly reserved for paid subscribers. The first part of the post is free to all, and then we get into details for subscribers.
There are many rules to laying out the features of a chip. At the modern limits of 5nm and below an extreme regularity is required, since this minimizes glitches in layout. Techniques like like pitch splitting are used which create half- or quarter-sized lines and separations, but which must be perfectly repetitive to optimize yield. This allows for creating fins for the FinFETs, by etching trenches down into the silicon base leaving fins separated.
Some of those fins will become P-channels (dominated by holes, mobile empty positions for electrons) or N-channels (dominated by mobile electrons). The fins may also have added germanium and be stressed, both features adding to electron mobility which makes faster and better transistors.
The initial process may create more fins than we really want, because the repetitive initial patterning is best with gaps in it. We are going to need some separation between the P and N fins, so an etching step cleanly removes a fin to create that separation. A set of N-fins and set of P-fins, with another separation between, will function as a “track” where complementary (CMOS) N and P transistor pairs are formed with the separator between them.
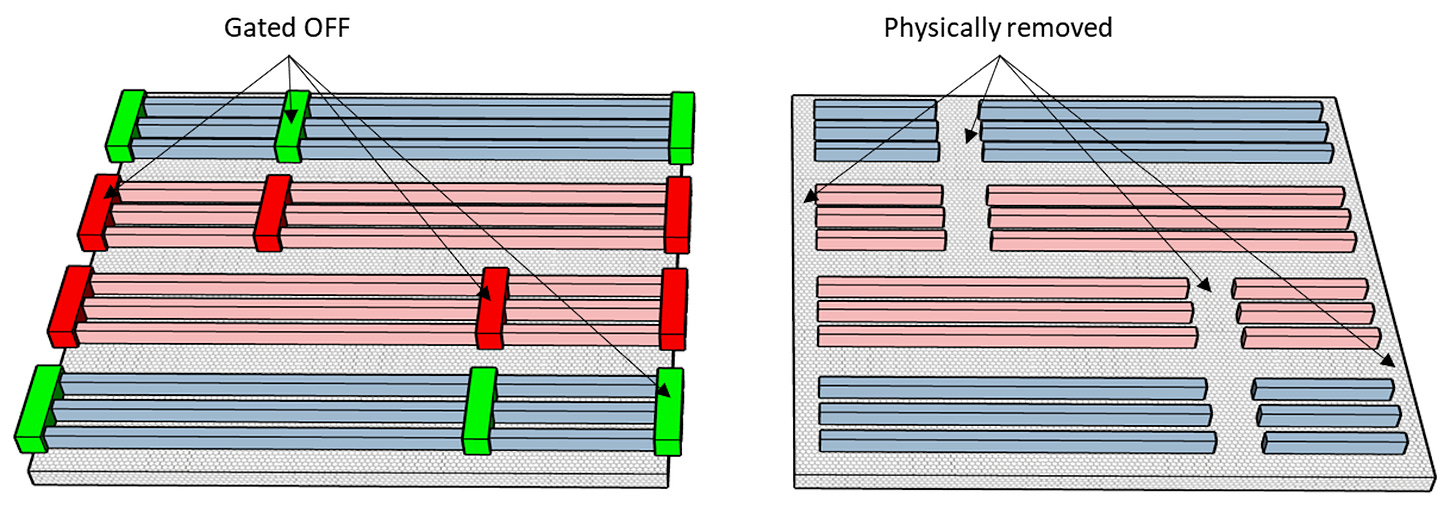
The fins need to have gaps where cells and transistors must be disconnected from their neighbors along the same track. The obvious way to do that is to physically etch to remove gaps where we want the disconnects. However, remember that the fins were stressed? Removing gaps can remove the stress, so another way to prevent connection is to add gates which are tied permanently to a power rail in such a way that the gate keeps the channel switched off, and non-conducting. The fin remains physically continuous, retaining the stress.
In all the diagrams I use physical gaps to visualize the disconnects, since drawing these fixed-off gates adds clutter and is logically equivalent to removing the fin. This is just one example of something you should keep in mind:
The cell images here are representations, not literally accurate, nor tested.
This blog will not teach you how to build a chip, but it will help you understand a chip.
Process Layers and their Rules
The chip features build up layer by layer. A simplified sequence begins with the connecting across fins to form sources and collectors for the transistors:
Notice again that each layer is very regular. They may start as continuous bars using pitch-splitting lithography to outline where the contact material is added, and then the gaps are imaged in another step which guides an etch to remove some material. The ends of the transistors are only allowed at regular intervals, just like the fins.
Next, the gates are added:
The alignment and pitch of the gates is chosen to fit them between the end contacts. You will see that the cell library never uses a gate without the source/collector separating it from neighboring gates along the fin. This cell library design assumes the source/collector sections are needed for uniform lithography spacing and consistent process steps.
The gates always connect across both N and P fins in this example, forming a true CMOS pair. However, it is allowed in the lithography for a gap to be etched separating the gates for the P and the N allowing them to be controlled by different signals. This is used in just a few places in the cell library, like the multiplexor:
In any “deposition” or “etch” there may be multiple steps. For example, a source/collector contact may be preceded by some doping of the exposed fin, adding an ALD contact enhancer, adding the contact, and then covering with an insulating barrier. The gate may use 2 or 3 layers of ALD with different materials to form an advanced dielectric and maybe different metals for N and P gates to select different work functions for the transistor bias. While fascinating, the details are out of scope here. All I want to convey here is a set of simple geometric constraints on what we can do with fins, transistors, and gates.
Adding Metal (Interconnect) Layers
The interconnect rules here were inspired by the "Intel 4" published information. The metal layers start off matching the fins and gates in spacing – and in requirements for purely linear shapes in fixed locations - which enables some efficient layouts since the connections can be as dense as the functions. Each level of connection requires a pair of layers to be formed – first a set of “vias” (vertical connections between levels), and then a layer of wiring on top of the vias.
The first layer of vias (V0) contact down to either the gates or the source/collectors. I have assumed both are allowed but they must be spaced far enough apart to avoid blurring together in the lithography. The metal layer (M0) runs along the same lines as the fins, including the lines of base fins which were removed for spacing.
The M0 layer is used to provide consistent power rails at top and bottom of a track. Tracks alternately mirror each other so that they can share power. The vias connecting to power are elongated, which is a pure fiction since there is no public documentation on how the connections are made without breaking rules on source/collector separation between the tracks. If the V0 lithography rules cannot stretch the vias like that (the lithography may be highly optimized for compact points) then a tool like Applied Sculpta may help. I simply assume there is a solution, but I also give that solution a “keep out” zone blocking the use of M0 in the lane where a power connection must be formed. It is interesting to see that Intel are switching to backside PowerVia which allows the power lanes to be used for signals. They demonstrated that with an Intel 4 variant but have not said it will be used for production products on the 4 node. So, I have not used it here. It looks seriously useful and maybe someday I will revisit cell library layout for Intel 20A or 18A which will use PowerVia.
The M0 level, apart from power, is assumed to be used only for the internal design of cells. The next level of interconnect, V1 and M1, runs parallel to gates and is available both inside cells and to route between cells.
We continue upwards to the V2/M2 interconnect which runs parallel to the fins but has a coarser pitch, 1.5x larger.
These were all the levels that were needed to lay out the cells I chose for the library. As we go up the V3/M3 and V4/M4 interconnect levels will be assumed to have the same spacings as the V1/M1 and V2/M2 levels, and that is all I expect to need for laying out a single bit column.
Who Has Precedent?
I do not cite an author for any of the cells here. You can find circuits in books, and occasionally they discuss the originals. Boole worked out some of the basic logic 200 years ago, and the Babbage difference engine had advanced concepts like carry-forwarding over 150 years ago, though it was done with mechanical gears and levers. The telegraph era soon introduced relays, so you will find the precedents for all things in this cell library except dynamic latches and clock edge pulses, were in relay form in telephony switches and computing engines in the 1930s. Vacuum tubes and transistors have similar on-off function to relays, and they all generally used resistive loading and one-sided switching. The final simplifications occurred when CMOS was introduced which had plenty of transistors and an elegant way of doing opposite switches driven by the same signal, so by the early 1980s every logical circuit in this library, now including dynamic functions, was in use in CMOS chips. Most chips of that era were implemented as trade secrets but were soon inspected by competitors and all the simplest forms were soon known at least 40 years ago. Original inventors may never be identifiable.
We begin cell designs below the divider for paid subscriptions. Each week will have part of the blog open to all, then details then below a divider. The open part will help you judge if the work is of value to you, and I will try to keep it interesting by itself.
Thank you for supporting this work!
The Simplest Cells: Inversion and Buffer
Transistors have a natural preference to be inverters. When the gate of an N transistor goes high (positive, Vdd) it switches on the channel having the effect of draining current towards low (negative, Vss). Conversely, to enable P transistor the gate is pulled low and the channel opens up flow of current bringing the output positive (towards Vdd).
These conditions are opposite. When the input signal is high, only the N transistor is on. The P transistor is off, so the current passing through the N transistor is coming from the load. A low input is the opposite: P transitor on, N transistor off. This is why CMOS is low-power: it does not waste power by having both transistors on at the same time. There are some edge cases with leakage (transistors in the off state for low-voltage designs are still carrying about 1/100,000th of the full current) and for the brief moment when an input is changing and both transistors are slightly on (less than 1/100th of full current). These matter for some designs, but not for the BlockChain miner chip, as will be explained in a later post.
Thus, the simplest circuit to build is an inverter, logically a NOT. Sometimes they are used for the not logic, but they are also useful as amplifiers where the output may be more powerful than the input. In figure 10 circuit (a) is shown with conventional symbol arrangement, while circuit (b) is exactly the same but the transistors have been rotated so the channel runs in the same direction as a real fin, to give a better idea of how the circuit is mapped to a cell. In circuit (c) this physical orientation is used to show how an inverter can be built both to left and right of a shared power source to give a compact double-strength output, and shared power like this is quite common. It can also be shared by unrelated functions as in (d) where left and right are both inverters but they invert different signals.
In the example in the video the input A is applied to gates on both sides of the power, and the output ~A ties together both sides to get a stronger drive. If less amplification is needed just one side could be used. So you might have left for A => ~A, while on the right there is B => ~B, or even some completely separate set of logic that uses the power.
Figure 11 continues with the sideways transistors showing how buffers use the left and right sides is to chain, resulting in an identity operation with signal gain, also known as a buffer: A => ~(~A). In figure 11(b) 3 outputs are tied together for stronger gain. If you look closely you might wonder “3 outputs? Only 2 outputs are tied to Aout.” This is another example of physical sharing. One of those source/collectors is fed both from left and right, so two of the three transistors share their output.
In remaining circuit diagrams the transistors will be back to vertical and less cluttered with physical puzzles, while videos and images will show the actual optimizations. You should practice with these simple circuits to see how various physical arrangements can result which share features or simplify wiring.
A detail you may notice in the video is that A and Aout appear to extend longer than needed to contact the structures below. This is done to indicate their freedom to connect upwards either for incoming or outgoing wiring. Occasionally we will find lengths are restricted, but the designs will always seek to ensure there is some flexibility in placement for inputs and outputs.
The Universal Bases for Logic: NAND and NOR
The next step up is negation, but with two inputs. These are NAND2 and NOR2:


These are vertically-flipped mirrors of each other, they would look the same if we flipped the power rails on one of them. If you learned logic design you know that everything logical function can be reduced to these gates, but that is not always a good way to use transistors. The rest of the library is cells where some trickery gives an advantage over the equivalent circuit formed of these primitives.
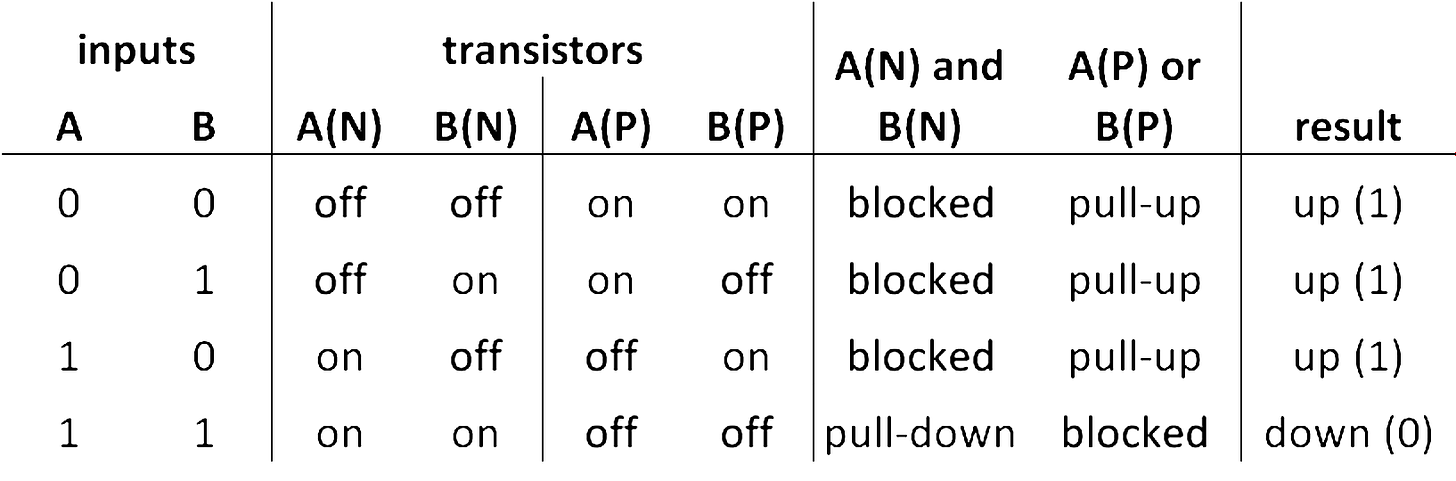
The following table explains how the transistors combine to deliver NAND logic:
If you want to understand how a circuit works it is a good idea to practice building a table like that. You will quickly see how the circuits work, mostly you will discover that some basic patterns of parallel or chained transistors are re-used in combinations to get the desired logic.
Here are the 2-gate NAND and NOR 3D views:
The outputs from NAND and NOR are interesting. They are single strength drives, but you can see that we needed to go up to Metal 1 to connect the upper and lower halves of the output source/collector. The limitations of lithography, even with EUV, at these modern feature sizes mean that patterns are strictly linear, or vias, or linear in the orthogonal direction. Back in the days of classic planar transistors, 28nm and above, it might have been fine to add a cross-connect at the M0 level, but going to modern sizes we have lost that freedom.
The 3-input NAND3/NOR3 are stretched versions of the 2-input:
NOR3 is again the mirror of NAND3 with Vdd and Vss flipped, as seen with 2-input NAND and NOR.
In the video, notice that the A input to the NAND3 must be kept away from the power rail, since it is assumed there is an M0 keep-out zone near to the power contacts. The 4-input versions NAND4/NOR4 are stretched some more:
That is the most we stretch in this library. The 4-input cells require a chain of 4 channels to pass a signal, and that is the limit we draw on acceptable single drive strength, because it is a reasonable rule of thumb without going into SPICE details of the analog behavior. Wider gates will need to be built from multiple basic cells, which will likely have negligible impact.
The next post will cover non-primitive functions which have nice optimizations. These include or-and-invert, 4-input AND and NOR, xor, multiplexing, majority, and some latches.