Error Correction in DRAM
Not always what you think it is
Hi folks, thank you for your patience. I started working with SemiAnalysis.com in July and it has been a lot. Also very interesting. As I settle into it I will schedule keeping up with the blog more effectively.
I have not given up on using the GNSS satellite data for a gravity telescope to see the exact angle of the Sun when viewed by gravity. No real problems with that except the disruption of the new work. I will get it done.
Meanwhile, here is a quick essay on error correction codes and how they are used both effectively and ineffectively in memory chips.
A few years ago Linus Torvalds famously roasted Intel over lack of ECC (Error Correction Codes) for DRAM in consumer CPUs. Here we are more than 3 years later, with new memory (DDR5 and LPDDR5) and new chips, has it been fixed. The TL;DR is that it has been very slightly fixed to avoid the situation getting worse, mostly swept under the carpet, and marketted as if we have real ECC. Today we have very weak ECC on consumer systems, not strong enough to make memory trustworthy.
What is ECC?
ECC adds extra bits to memory which contain the result of a calculation on your data. If your data has not been corrupted, the pattern calculated when reading the data should match the result appended to your data. This is a bit like the check digit on your credit card which is used to help detect simple typos. Now, imagine that we see the check digit is wrong, so we start changing the digits until we get a correct check digit. That is not really a good idea with your credit card because the check digit can be fooled by changes to almost any digit, but this is the intuition behind ECC. Can we make a checking system strong enough to tell us not only that there is a mistake, but also to reliably show us what the mistake is? This would be an error correction code, or ECC. And yes we can do that, though all such schemes have their limits.
The most simple ECC scheme, which is also widely used and good for simple cases, is the Hamming Code.
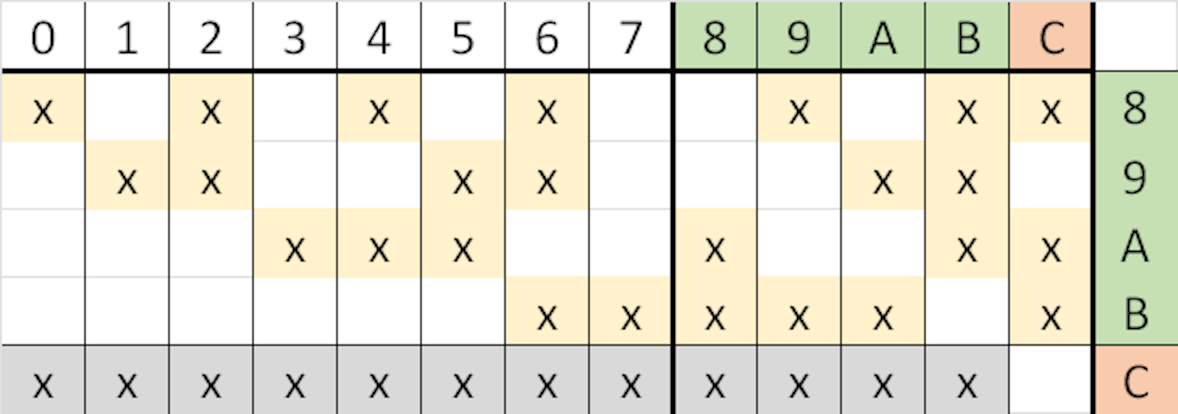
There are general forms of this which can correct multiple errors, but by far the most common Hamming code can correct just 1 bit in a binary sequence. It does this by taking the XOR of every bit, every second bit, every 4th bit, every 8th bit, .., until it gets to a power of 2 which is longer than the binary sequence. These bits form a number, the parity code, which is appended to the sequence. Now if just one bit is flipped and the parity code is recalculated, if the new code is XOR’d with the appended original parity code to give a “syndrome” value, the syndrome is the bit number of the fault. We can get the original back by flipping that one bit.
In the example above there are 7 data bits and 5 correction or “parity” bits. The “x” indicate that a bit in that column contributes to parity in that row. You will see the rows feed into bits 8..B, which are the 4 parity bits, and a 5th bit C which is used for double error detection.
See what happens if bit 4 gets flipped by a fault. When we do the new parity calculation after reading the error value, bits 8 and A will not match the original parity which we read, so we can see that a parity value difference (syndrome) of 5, which matches the Xs for bit 4, so bit 4 needs to be repaired (by flipping). We also see that bit C did not match, exactly as we expect for a single fault.
Try with 2 bits flipped, let’s keep the fault in 4 but add another fault in bit 0. Now the parity mismatch syndrome value 4, pointing to bit 3. However, Parity bit C flipped twice and is back to no flip, which is the alarm for Double Error Detection when 9..B do show some change. We conclude that the error is uncorrectable (there are several 2-bit faults with the parity mismatch of 4).
Unfortunately if there 3, 5, 7, 9, or 11 faults parity bit C will confirm a flip and we will trust the correction, which is wrong. For all ECC schemes: you must know the error model when deciding if the ECC is trustworthy. In this case we need to understand the if there is any risk of more than 2 faults.
In most error correction systems you will have exponential growth in costs for perfect correction, but detection of failure is relatively cheap. So, most real-world ECC systems spend reasonable resources on correction and then add some small resources to detect remaining failures. The users of imperfect systems should have a strategy such as retry to work around the uncorrectable failures.
The confidence we have in knowing that an error correction is not itself a mistake is the “probity” of the ECC. For example, a correction system including a final CRC of 8 bits might have a probity of about 99.5%. In a system making 1 risky correction per year (risky means trying to correct an error which is larger than the ECC can fix) that means about 200 years before a silent error. In a system making 1 risky correction per second, you have a silent fault every 3 minutes. You might want a 32 bit CRC for that.
Knowing the error model - what causes faults - is important when estimating how often your ECC will be overwhelmed. That can guide deciding how strong the probity needs to be in avoiding silent acceptance of a failed correction.
An example of a system where the error model is suitable for SECDED is the SRAM inside a logic chip. SRAM is susceptible to radiation events that flip a bit. These are rare but real, even at sea level. More common at places like Denver, Mexico City, or La Paz. Seriously common in space. However, the circuits are vulnerable at very specific places. A radiation event releasing a cloud of charge right there will flip one bit. Two bits are very rare, and it is (pun intended) astronomically unlikely to flip 3 bits. So, a SECDED Hamming code on internal SRAMs is a good design to handle this error model, where even that one DED bit gives excellent probity.
DRAM storage is a more difficult problem
The error model for using DRAM is not simple. The model includes:
failures on the wires of the interface. These can be due to noise margins in the modulation, which for NRZ will be 1 or 2 bits, but also errors due to interference pulses that could knock out more than one bit on more than one wire.
single bit failures inside the DRAM while the data is stored. Sometimes a single cell itself is broken, but most often these are temporary problems where the cell leaks its contents before refresh.
multiple bit failures within a bounded region. These occur when there is something wrong with a structure, like a word-line within a sub-array of cells, may affect a group of bits in a given transfer. 16 bits is commonly the bound as this is the number of bits from one subarray in a typical transfer. Breaks and shorts in a single wire connecting the host to the DRAM may also be bounded - beginning with DDR5 and LPDDR5, the designers should take care to match the wires to have the same bounds as the most likely internal bounded faults so a single wire transfers 16 bits at most.
multiple bits in an unbounded region. These occur when any higher-level structure of the chip fails. This can be an entire word line over multiple sub-arrays, a fault in the addressing logic, a fault in the periphery processing the data, or a break or short in multiple wires connecting the host and DRAM chip.
multi-chip faults. In some cases multiple DRAM chips may be mounted on the same DIMM or inside the same BGA package. Corrosion, stress cracks, power dips, or support chip failures may cause multiple DRAM chips to fail.
We can say this is the error model for DRAM. Crucially, multibit faults are not simply coincidental single faults. That would have been sweet, because combining two separate faults is really, really unlikely. Unfortunately, multibit faults have their own causes, and they seem to add up to about 10% of all faults as observed in a careful recent large-scale study. Some of those are unbounded faults which no ECC can fix, so we also need probity. We need to know when the data we read is poisoned (faulty and could not be fixed).
Reed-Solomon to the Rescue?
The usual code chose to match the DRAM error model is called Reed-Solomon. This code was invented 60 years ago and is useful to fix multibit symbols. In the case of DRAM the symbol size is 8-bit bytes. Typically with DDR memory the code covers 16 bytes of data and has 4 bytes of correction code. The code can correct any 2 bytes at fault, and 2 bytes of the code are used up in making the location calculation. If the fault covers more than 2 bytes it has about 99% probity, about 1% of those overwhelming faults will silently fool the code.
I have a GitHub project if you want to dive deeper on Reed-Solomon ECC.
A CPU generally reads 32 bytes of data so each half of the data gets its own ECC. Overwhelming errors quite likely show up in both halves, so the chance both will be fooled is a little better than for one transfer.
Sounds good, right? The problem is, that system was designed for DDR on DIMMs. It is not available on single-chip memories like LP-DDR, and it only began to be used for HBM beginning with HBM3.
The HBM2 and LPDDR specs mention ECC
So we are good, right? No, there are three problems:
What is the ECC is actually correcting?
Does the correction match up to the error model?
Is there any probity - are uncorrectables reported?
All three get a failing grade.
First, one kind of ECC available is called “inline” ECC. This is the one you find in the specs included as an alternative to the Dat Bit Inversion (DBI) function. When you enable the ECC variation they correct bits on the wire - they are what is usually called a Forward Error Correction (FEC) on data transport codes. This can give you more reliability on the wires, but it does nothing to correct errors that occur inside the DRAM, and it is only useful for single bits. Better than nothing, but it does not match the true error model.
The second kind of ECC was introduced in LPDDR4-x and LPDDR5, and that is an on-chip correction of single bits. This handles roughly 90% of the error model, nice but not strong.
This internal single-bit ECC has no probity whatsoever. While it does have a partial detection of 2 bit errors, it has zero provision to report that to the host. The attempted correction is logged on the DRAM for later analysis but the host gets no warning of poison data at the time it reads it. So, roughly 10% of errors will be silently uncorrected. This is a terrible mismatch to the error model.
One is the Loneliest Number
In general single chip DRAM has struggled with ECC. DDR on DIMMs provided ECC only by adding extra chips. This is a really wasteful solution. In DDR5 you have 10 chips doing the work of 8. The same command are repeated by all chips and the chips tend to be in random access mode because 8-chips in parallel need only 1/8th of the sequential length per transfer. Not to mention those extra 2 chips - when the on-chip single-bit ECC is included, DDR5 uses over 33% of capacity to provide ECC.
One-chip solutions have a lot going for them. LP-DDR has 4x the IO bandwidth per chip compared to DDR, and each chip can operate on separate commands so that the same capacity of LP-DDR can keep about 4x as many threads active as with DDR.
Despite being packaged in stacks, HBM is also a single chip solution. Each command to an HBM stack is sent to only one of the chips, which uses 128 bits of IO for the data transfer. So, per chip, HBM is about 8x the transfer rate of LP-DDR and handles the same amount of parallel activity.
A lot will be expected from LPDDR and HBM, but for ECC they need a system that works well for each single chip.
How Reliable does DRAM Need to Be?
DRAM is pretty reliable. The best field study of DDR4 reliability showed raw failure rates around 100 Failures In Time (FIT, failures per billion hours) per 2GB chip. Your cellphone may use 8 of those chips, so you accumulate roughly 34,000 chip-hours per year. You could expect to run about 300 years between failures at the rate seen in the Google & AMD study. Even if phones are a little worse, the occasional scrambled photo or email is not a catastrophe, and phones have other sources of error that may be more important. This level of success is why ECC is not found on LPDDR4 or earlier, and why only weak ECC was recently added.
A similar rationale applies to HBM1 and 2 which were mostly designed for graphics where a pixel glitch or even a wrong texture may go un-noticed and not be considered as important.
What has changed is that some new uses for the low power and better bandwidth of both LPDDR and HBM have caused much larger chip counts to be used and made the consequences of failure more important. LPDDR and HBM are moving up into the big leagues, and for some purposes may be more important that the older DDR.
If we look at the Apple Mac Pro Ultra, it has 96 LPDDR5 chips. The next generation Nvidia Grace will have 256. These may put in 800,000 or 2,000,00 chip-hours of use per year, enough to generate an 8% to 20% chance of raw error. The data they work with is valuable and generally needs to be correct.
If the LPDDR5 on-chip single-bit error correction is removing 90% of errors then the faults come down to 1 to 2% rate. However, if no further measures are taken, all of those errors would be silent. The applications would have no indication of poison and would not be able to take evasive actions like repeating the work for an uncorrectable error.
HBM3 and LPDDR6 are better
HBM3 has added ECC for correction of 2 bytes out of 32, and it has pretty solid probity using a 16-bit CRC. Strictly speaking the host could choose to use less than 16 bits for the CRC, it could use some bits for metadata, but the combination of 99% probity on the Reed-Solomon with even a short CRC is still pretty strong.
LPDDR6 announcements show some weak ECC additions. There are two fields in LPDDR6 which are associated with ECC. One field is useful only for FEC on the wiring, and can only correct one bit failures. The other field, however, is usable for true ECC, offering 16 bits of extra storage for each 256 bits of user data. This is only enough for correction of 1 bit error with 99.5% probity. Better probity than LPDDR5 (which scored zero on probity) but no improvement in error rate. At least the errors will rarely be silent.
Things get more interesting if the host chooses to combine the extra bits from a double or quadruple transfer. High performance host chips generally want 512 or 1024 bit transfers. It is possible to run Reed-Solomon correction if the extra bits are combined as a 32-bit or 64-bit ECC. The 32 bit version can correct 2 bytes of error in 64 bytes (512 bits) of data, with about 95% probity. This would be a solid improvement for LPDDR since the 2 byte correction will cover about 98% of errors, and then probity of 95% will avoid most silent errors. The correction potential becomes outstanding for 128 byte (1024 bit) data tranfers where 4 bytes could be repaired with better than 99.9% probity if a single 64-bit ECC calculation is used. That would, however, be quite a computational challenge in silicon size and latency, os it is more likely that a double 512/32 bit ECC will be used.
How expensive will this be?
The startling thing is that LPDDR6 could implement this essentially for zero extra cost. This is because LPDDR5 already uses 16 bits per 256 for its internal ECC. It just uses those bits very weakly, organizing them as two sets of 8 bits per 128 data. That supports single bit correction with no probity, because the extra bits are not “round tripped” to the host.
In LPDDR6 it is possible to simply make the round trip happen, putting those same bits to much more effective use. The host generates the parity, and the host verifies the parity, so it can use larger ECC codes and the host can calculate a probity check to avoid almost all chances of poison.
In practice not enough of the LPDDR6 spec has been revealed to the public. JEDEC is highly secretive. It is possible they keep the older internal 16 bit half-effort and then layer the round-trip 16 bits on top. That would be a real shame, since they waste another 16 bits of the new data transfer for much less value, and if they really have put 32 bits of extra data inside the chip they should round-trip it all. We will not know exactly what happened until the LPDDR6 spec is fully published.
In Summary
LPDDR4 and 5 do not have strong enough ECC for applications requiring high reliability and correctness. Systems using those chips should use some of the data capacity to add additional fault detection.
HBM 1 and 2, the same. Add data overheads for additional safety if you need to be correct.
HBM3 introduces stronger correction and reasonable probity. Watch to ensure this is maintained or improved for HBM4.
LPDDR-6 finally plans to introduce a level of ECC and probity which we could have had for no extra cost in LPDDR5.
JEDEC secrecy and unaccountability is inadequate for a standards body which controls the design of products essential and ubiquitous in modern life. It has been using misleading naming and threadbare descriptions of ECC features, and it has adopted weak designs. The error model needs to become clearly explained in the spec and quantified in product design, and JEDEC needs to take error correction and probity unapologetic first-rank goals in future devices.